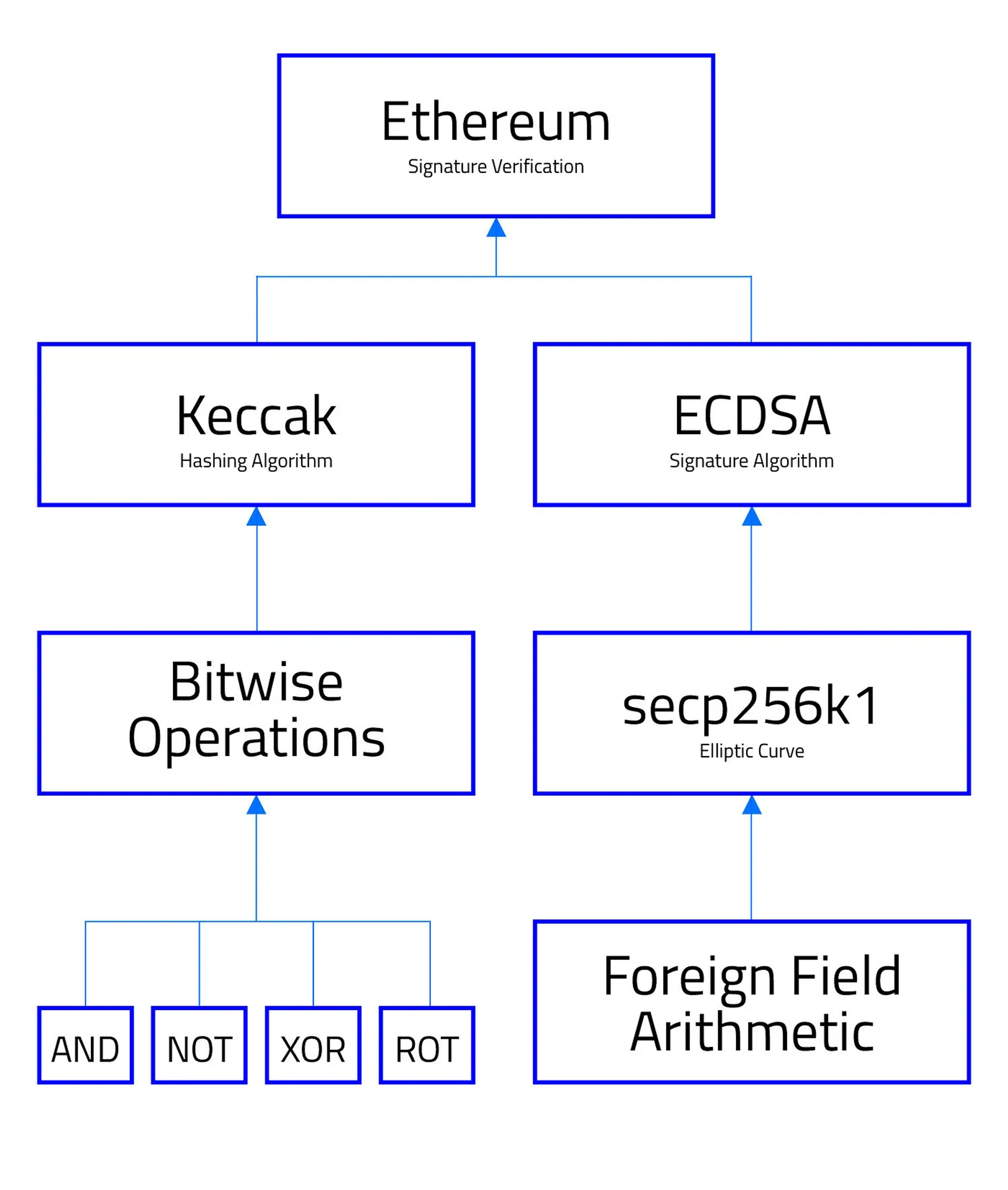
The v0.15.1 release of o1js (What’s New in o1js: January 2024) added some of the most community-requested features yet: the ability to verify Ethereum signatures using the Elliptic Curve Digital Signature Algorithm (ECDSA) and hashes using Keccak. There’s good reason for this long-standing request. The ability to verify ECDSA signatures in o1js allows developers to build zero knowledge applications that incorporate activity from Ethereum and other EVM blockchains, or to add layers of scalability and privacy to existing applications in those ecosystems. We were eager to provide these capabilities as soon as possible but we knew that it would be a substantial undertaking to do it properly. Zero knowledge cryptography has some specialized components that are often incompatible with other forms of cryptography, especially given our proof system’s native ability to support recursive composition. Resolving this would require the support of lower-level features that are useful tools in their own right. And, if these tools were sufficiently abstracted, they would provide a kind of skeleton key that also unlocks interoperability with many other cryptographic systems! This ambitious approach resulted in a cascade of dependencies.
Ethereum combines the ECDSA signature and Keccak hashing algorithms to sign and verify transactions. ECDSA uses an elliptic curve called secp256k1, which is built on a finite field different from the one o1js was designed around (the Pallas base field). So, to get ECDSA, we needed to implement a mechanism for working with foreign finite fields and foreign elliptic curves over those fields. Keccak also presented a challenge since it is comprised primarily of boolean logic, which, although efficient in physical computers, is generally quite expensive in zero knowledge proof systems. So, to get Keccak, o1js also needed efficient, provable bitwise operations.
Bitwise Operations
Keccak uses four specific bitwise operations: NOT, AND, XOR, and ROT. Modern processors support these operations directly at the hardware level, which makes them exceptionally efficient on most silicon. But computation works differently in zero knowledge proof systems. Any operation that o1js can prove must be represented as arithmetic over the native field, and the naive approach to this is incredibly inefficient. We needed versions of these operations that were optimized for proving.
The specific implementations of each operation are relatively intricate (you can learn more in the Mina Book if you are interested), but in short, XOR and ROT are both implemented as custom gates within Kimchi, whereas NOT and AND are implemented as gadgets using XOR and the generic gate.
1// Using provable bitwise operations:
2
3// and(a: Field, b: Field, length: number) => Field
4// will compare `length` bits
5let a = Field(0b0011);
6let b = Field(0b0101);
7let c = Gadgets.and(a, b, 4);
8c.assertEquals(0b0001);
9
10// not(a: Field, length: number, checked: boolean) => Field
11// will compare `length` bits
12let a = Field(0b0101);
13let b = Gadgets.not(a,4,true);
14b.assertEquals(0b1010);
15
16// xor(a: Field, b: Field, length: number) => Field
17// will compare `length` bits
18let a = Field(0b0101);
19let b = Field(0b0011);
20let c = Gadgets.xor(a, b, 4);
21c.assertEquals(0b0110);
22
23// rotate64(field: Field, bits: number, direction: 'left' | 'right' = 'left') => Field
24// rotate32(field: Field, bits: number, direction: 'left' | 'right' = 'left') => Field
25// will rotate a value in the specified direction by the specified number of bits
26let x = Field(0b001100);
27let y = Gadgets.rotate32(x, 2, 'left'); // left rotation by 2 bits
28y.assertEquals(0b110000);
29
30// same as rotation except that bits fall off the end instead of wrapping around
31// leftShift64(field: Field, bits: number) => Field // input must <64bits
32// leftShift32(field: Field, bits: number) => Field // input must <32bits
33// rightShift64(field: Field, bits: number) => Field // input must <32bits
34let x = Provable.witness(Field, () => Field(0b001100)); // 12 in binary
35let y = Gadgets.leftShift64(x, 2); // left shift by 2 bits
36y.assertEquals(0b110000); // 48 in binaryEach of these new bitwise operations uses far fewer constraints than their naive counterparts would, and provide efficient build blocks for many other provable operations. We could use them to add other hash functions to o1js in future. They have a wide range of applications beyond cryptographic primitives too. In fact, members of our community have previously written inefficient versions manually to do things like evaluate the state of a game.
Keccak/SHA-3
With the bitwise operations in place, we were poised to start working on the Keccak hashing algorithm. Since Keccak operates over a string of binary information, we created a new provable type called Bytes, conveniently initializable from many other commonly used types. This type allows those provable bitwise operations to be performed over arbitrary, fixed-length arrays of bytes, enabling an efficient implementation of Keccak.
1// Using Keccak and the Bytes class to hash a string to various output lengths:
2
3// define a preimage
4let preimage = 'The quick brown fox jumps over the lazy dog';
5
6// create a Bytes class that represents 43 bytes
7class Bytes43 extends Bytes(43) {}
8
9// convert the preimage to bytes
10let preimageBytes = Bytes43.fromString(preimage);
11
12// hash the preimage
13let hash = Hash.SHA3_256.hash(preimageBytes);
14
15console.log(hash.toHex());
16//69070dda01975c8c120c3aada1b282394e7f032fa9cf32f4cb2259a0897dfc04
17
18// Keccak and SHA-3 implementations are available for outputs of 256, 384, and 512-bits.
19Hash.Keccak256.hash(bytes);
20Hash.Keccak384.hash(bytes);
21Hash.Keccak512.hash(bytes);
22Hash.SHA3_256.hash(bytes);
23Hash.SHA3_384.hash(bytes);
24Hash.SHA3_512.hash(bytes);Our native hashing algorithm, Poseidon, was designed to be as efficient as possible in zero knowledge proofs and is still the best choice in most situations due to its compatibility with our native finite fields. When you need to interface with external cryptographic systems, however, provable hashing with efficient bitwise operations can make it possible. In this case, Keccak and SHA-3 allow provable verification of Ethereum state hashes, and can even interact with non-blockchain applications like document signing and traditional web protocols.
Foreign Field
In contrast to Keccak’s bitwise operations, ECDSA operates on an elliptic curve that is defined over a finite field. The same is true of many zero knowledge proof systems, where the specific finite field in use generally offers many benefits to performance and ease of use within that proof system and is known as the native field. However, proof systems have special demands not found in most other cryptographic systems, and differing finite fields are not interoperable. This brings us to the problem: ECDSA uses a different curve to Kimchi, the proof system behind o1js. Kimchi uses the Pasta curves, chosen for their suitability to recursive zero knowledge proofs. ECDSA, on the other hand, uses secp256k1. This is a good thing, given their different functions, but it presented a compatibility issue. We needed to support a foreign curve that is built on a foreign finite field.
To generalize this need for interoperability with standardized cryptography like the secp256k1 curve used by ECDSA, we created the new `ForeignField` class. It allows developers to define new fields with any modulus less than 2²⁵⁹ and is efficient enough to unlock a variety of new use cases. It’s also pretty easy to use!
New foreign fields are created by extending the `ForeignField` class and passing in the desired modulus (the size of the field) as an argument.
1// Creating a foreign field with modulus 17:
2
3class Field17 extends createForeignField(17n) {}You can then use the resulting foreign field class the same way you use the native `Field` class. It exposes many equivalent methods, each behaving as you would expect (but for a different field, of course).
1// Performing modular arithmetic over a foreign field:
2
3let x = Field17.from(16); // create new element of the field equal to 16
4x.assertEquals(-1); // 16 = -1 (mod 17)
5x.mul(x).assertEquals(1); // 16 * 16 = 15 * 17 + 1 = 1 (mod 17)
6
7// do any of the following opperations
8x.add(x); // addition
9x.sub(2); // subtraction
10x.neg(); // negation
11x.mul(3); // multiplication
12x.div(x); // division
13x.inv(); // inverse
14x.assertEquals(y); // assert x == y
15x.assertLessThan(2); // assert x < 2
16let bits = x.toBits(); // convert to a `Bool` array of size log2(modulus);
17Field17.fromBits(bits); // convert back
18
19// non-provable methods
20let y = SmallField.from(5n); // convert from bigint or number
21y.toBigInt() === 5n; // convert to bigintDespite the apparent simplicity and ease of use, a lot is happening beneath the surface! It’s impossible to represent a field with a modulus larger than that of our native field. Instead, each foreign field is represented by three base field elements. There are also three variants of the `ForeignField`, each imposing a different set of constraints on the underlying representation. You can learn more in the Foreign Field Arithmetic section of the Mina docs.
We also created a class called `ForeignCurve`, which is essentially a layer on top of `ForeignField` that lets you interact directly with a curve defined over a foreign field in the same way that you would interact with a `Group` defined over the native Pallas curve. It works just like `ForeignField` except that instead of passing in a single modulus, you pass in an object with all the parameters of the desired curve. We’ve included a few common curves in o1js already, but feel free to open a PR if we don’t have what you’re looking for yet.
ECDSA
ECDSA is fundamentally just a sequence of elliptic curve operations used to construct or verify a signature (which is really just a point on the curve). And now, with foreign field and foreign curve support, it’s relatively easy to implement ECDSA over secp256k1.
1// Creating and proving the validity of an ECDSA signature over the secp256k1 foreign curve:
2
3// create a secp256k1 curve from a set of predefined parameters
4class Secp256k1 extends createForeignCurve(Crypto.CurveParams.Secp256k1) {}
5
6// create an instance of ECDSA over secp256k1
7class Ecdsa extends createEcdsa(Secp256k1) {}
8
9// a private key is a random scalar of secp256k1 - not provable!
10let privateKey = Secp256k1.Scalar.random();
11
12// a public key is a point on the curve
13let publicKey = Secp256k1.generator.scale(privateKey);
14
15// sign an array of bytes - not provable!
16let signature = Ecdsa.sign(bytes, privateKey.toBigInt());
17
18// sign a hash of a message - not provable!
19let signature = Ecdsa.signHash(hash, privateKey.toBigInt());
20
21// verify a signature
22let isValid: Bool = signature.verify(message, publicKey);
23
24// verify a hash of a message
25let isValid: Bool = signature.verifyHash(hash, publicKey);These new capabilities give zero knowledge applications written in o1js the ability to verify Ethereum signatures, which unlocks a range of use cases. By exposing the lower-level building blocks, we’ve also set the stage for further interaction with other cryptographic systems. We look forward to seeing what you build using these privacy-preserving interoperability features!
Check out the docs for ECDSA, Keccak, foreign fields, and bitwise operations to learn more. Or jump on Discord with feedback and questions. We’d love to hear which features you want to see next.


